[고차원 데이터분석] MCP와 SCAD (Bias reduction technique) (2)

 지난 포스팅에 이어 MCP와 SCAD를 다룬다. LASSO와 마찬가지로 MCP와 SCAD는 Design matrix가 orthonomal한 경우 closed form solution을 가진다. 이 때 MCP와 SCAD의 univariate solution은 다음과 같다.

---

• MCP thresholding (firm thresholding) :

$$ F(z | \lambda, \gamma ) = \begin{cases} \frac{\gamma}{\gamma-1}S(z|\gamma) & \text{if $|z|\leq \gamma \lambda $}\\
z & \text{if $|z| > \gamma \lambda $}
  \end{cases} $$

where $\gamma > 1$

 

• SCAD thresholding :

$$ T_{SCAD}(z | \lambda, \gamma ) = \begin{cases} S(z|\lambda) & \text{if $|z|\leq 2\lambda $}\\
    \frac{\gamma -1}{\gamma -2}S(z|\frac{\gamma \lambda}{\gamma-1}) & \text{if $2\lambda < |z| < \gamma \lambda$}\\
z & \text{if $|z| \geq \gamma \lambda $}
  \end{cases} $$

where $\gamma > 2$

---

 여기서 z는 X가 orthonormal 할 때 OLS solution이다. (즉, $\text{z}=\text{x}^{t}\text{y}/n$) 만약, $\gamma \rightarrow \infty$라면, $F$와 $T_{SCAD}$ 모두 Soft thresholding operator $S(\cdot |\lambda)$로 수렴한다. 반면 $\gamma \rightarrow \gamma_{min}$라면 $F$의 경우 Hard thresholding operator로 수렴하지만 $T_{SCAD}$는 그렇지 않다. 두 operator 모두 $\gamma$가 최솟값으로 접근함에 따라 불연속 함수로 수렴한다는 사실은 같다. 다음 그림은 지금까지 설명한 operator를 시각적으로 비교한 그래프이다. (Hard thresholding 은 빠짐)

---

 위에 언급된 thresholding의 개념을 배경으로 최적화(Optimization)가 어떻게 진행되는지 알아보자. LASSO와 마찬가지로 MCP와 SCAD는 CD(Coordinate Descent)을 사용한다. CD algorithm은 최적해에 수렴할 때 까지 모든 파라미터를 순회하면서 단계마다 하나의 파라미터만 업데이트를 한다. LASSO와 같이 목적함수가 convex일 경우 CD를 사용해 찾아진 solution은 global minimum을 보장한다. 다만 LASSO는 strictly convex가 아니기 때문에 multiple solution이 존재할 수 있다. 무튼 CD algorithm은 LASSO, MCP, SCAD와 같이 single parameter에 대해 closed form solution을 가지지만 multiple paramter에서 그렇지 않은 경우 굉장히 효과적인 알고리즘이다.

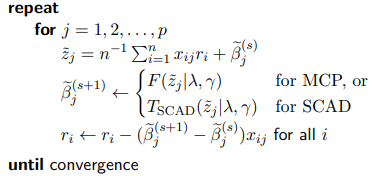
LASSO의 CD에서 Soft thresholding 부분이 $F$와 $T_{SCAD}$로 바뀐 것을 제외하면 동일하다. 하지만 LASSO와 달리 MCP와 SCAD는 folded concave penalty를 사용하기 때문에 convex function이 아닐 수도 있다. 따라서 convex가 아님에도 CD알고리즘을 사용해 solution을 찾으면 global minimum을 보장하지 못한다. MCP와 SCAD의 Objective function이 convex려면 다음과 같은 추가적인 조건이 필요하다.

---

• MCP :

$$\gamma > \frac{1}{c_{min}}$$

• SCAD :

$$\gamma > 1 + \frac{1}{c_{min}}$$

여기서 $c_{min}$은 $X^{t}X/n$의 가장 작은 eigenvalue다.

---

 하지만 고차원 세팅($n<p$일 경우)에서 항상 $c_{min}=0$이고 MCP와 SCAD의 목적함수는 전역적으로 convex가 될 수 없다. 그럼에도 다음의 시뮬레이션 결과를 보면 convex penalty가 항상 non-convex penalty보다 뛰어난 것은 아니다.

$\gamma \rightarrow \infty$에 따라 목적함수의 convex 정도가 증가함을 상기하자. 특히 파란색 시뮬레이션에서 목점함수를 더 convex하게 만들었음에도($\gamma$를 증가시켰음에도) MSE는 증가하는 것을 볼 수 있다. 이런 일이 발생하는 이유는 solution이 sparse하기 때문이다. 즉, p개의 모든 차원이 response variable과 관련이 있는게 아니라 이들 중 극히 일부만 signal로써 역할을 가지고 나머지는 차원은 noise나 다름없다. 만약 일부의 차원에 우리가 관심있는 차원들이 모두 포함되어있다면 그것보다 더 높은 차원에서의 local minimum의 존재는 고려하지 않아도 된다.